オープンスクール数学体験授業「17段目の秘密」 オープンスクール
対象 中学3年生 30名 45分授業 7月29日 10:45~11:30
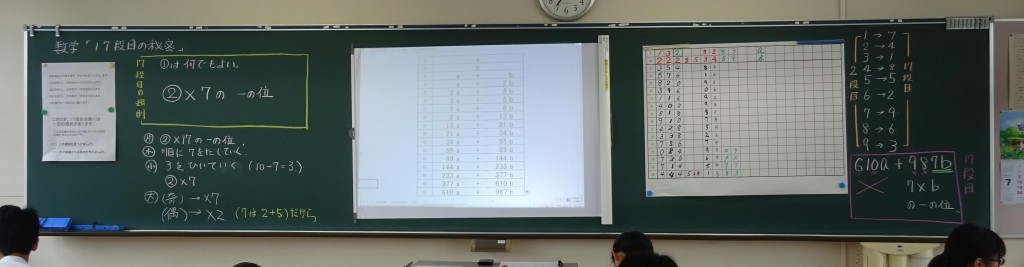
課題提示はppt、文字式での説明はexcelを使っています。
数学科課題学習「17段目の不思議」は、かつて玉置崇が「数学の授業を感動の連続に ~ シリーズ・魅力ある数学授業を創る」(明治図書)で実践報告したものです。各地で様々な追試実践がなされています。
授業の流れ
―学習課題―
自然数を2つ考えます。それぞれを①と②とします。
①と②をたし、その和の一の位を③とします。
②と③をたし、その和の一の位を④とします。
③と④をたし、その和の一の位を⑤とします。
この操作を17段目まで続けます。
このとき17段目の数には一定の規則があります。
(1) この規則を見つけましょう。
(2) その根拠となる理由を考えましょう。

最初に最前列の生徒を指名し、自由に自然数をいってもらいます。コントロールせずに授業を始めたかったのです。「1と2」言いました。①に1、②に2と書き、やり方を示しながら実際に計算すると⑰は4になりました。次は意図的にコントロールして①は3、②は2として自分で計算させ机間観察して、やり方の理解を確認しました。ここでも4になりました。
ここで、「いろいろ試して規則を見つけなさい」と指示しました。自己追究させます。2人指名し板書させます。多くの生徒が次も②を2として⑰が4になることを確かめました。気がついたことをワークシートに記入させます。②が同じ数なら⑰も定まった数になることに気づきました。①がどんな数でも②によって⑰が決まるようです。そこで対応表をつくります。
1→7
2→4
3→1
4→8
5→5
6→2
7→9
8→6
9→3
この対応表をもとに規則を考えます。

気づいた性質
・ ②に17をかけるとよい
・ 7をたしていけばよい
・ 3をひいていけばよい。
これらを全体で追究していく中で、「②に7をかけた数の一の位」であるとの結論を出しました。
これらの流れとは別に、「②が偶数の時は2をかける。②が奇数の時は7をかける。」と独自の規則を深慮している生徒がいました。最後に使おうと置いておきます。説明の段階に入ります。数学での説明は文字を使うことを確認した上で、①をa 、②をb として、それぞれの段をa、b を使って文字の式に表していきます。⑰は610a+987b となりました。aの係数が610だからaがどんな数でも⑰に影響しないこと、bの係数が987だから、9と8は⑰の一の位と関係がないので、7bの一の位が⑰段目の数になることを確認しました。最後に学習を振り返ります。
最後に「②が偶数の時は2をかける。②が奇数の時は7をかける。」について、7=2+5と考えると②が偶数の時は2をかけるが成り立つことを説明しました。
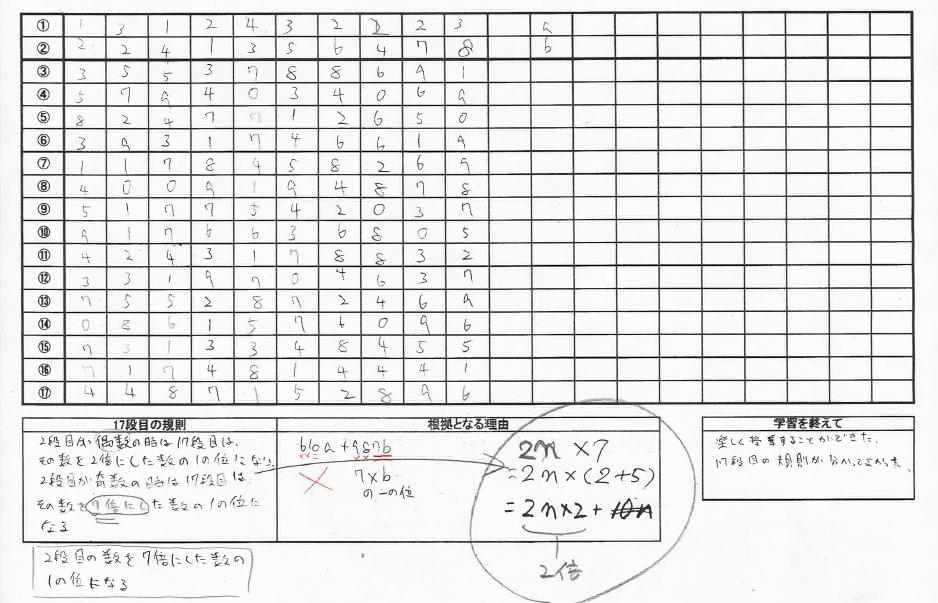
生徒の振り返り
○規則を知ることができて楽しかった。
○他の所には規則がないか考えたい。
○とても頭を使って考えたので疲れたけれど、おもしろい授業だったのでよかったです。
○すごく納得できた。他にも何かにたことができるか考えてみようと思った。
○楽しく計算できた。簡単な規則だった。
○根拠となる理由を考えるのに、簡単に説明できないと思っていたが、面倒なことを苦労して導き出すと簡単な結論になった。考えることは楽しいと思った。
○①②の計算をしているときは、全くわからなかったけど、規則がわかるととても簡単だった。
 投稿のRSS
投稿のRSS